Circuitos na pratica: Teoremas Thévenin e Norton

Teorema de Thévenin

Índice

O teorema de Thévenin estabelece que qualquer circuito linear visto de um ponto pode ser representado por uma fonte de tensão (igual à tensão do ponto em circuito aberto) em série com uma impedância (igual à impedância do circuito vista deste ponto).

A esta configuração chamamos de Equivalente de Thévenin em homenagem a Léon Charles Thévenin, e é muito útil para reduzirmos circuitos maiores a um circuito equivalente com apenas dois elementos a partir de um determinado ponto, onde se deseja, por exemplo, saber as grandezas elétricas como tensão, corrente ou potência.

Cálculo do Equivalente de Thévenin

O cálculo do Equivalente de Thévenin baseia-se no Teorema da superposição quando o circuito a ser reduzido é separado do circuito a ser estudado e as análises de circuito aberto e em curto-circuito são aplicadas para se conseguir as relações que permitam a redução desejada.

O Equivalente de Thévenin pode ser construído a partir de duas etapas:

1. Determinar a resistência ou impedância de Thévenin, também chamada de resistência ou impedância equivalente. Esta resistência (ou impedância) é aquela vista do ponto onde se deseja reduzir o circuito, e neste caso, com as fontes de tensão curto-circuitadas e as fontes de corrente abertas.

2. Determinar a tensão de circuito aberto no ponto onde se deseja reduzir o circuito.

Exemplo

No exemplo a seguir, é possível ver um circuito de corrente contínua sendo transformado pelo teorema de Thévenin no ponto A e B.

circuito original

Etapa 1: Cálculo da Resistência de Thévenin

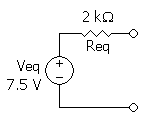
circuito equivalenteThévenin

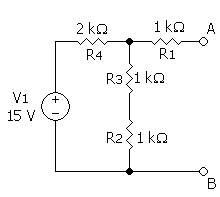
A resistência de Thévenin pode ser obtida pela resistência equivalente vista do ponto AB, neste caso, com a(s) fonte(s) inoperantes. Na Etapa 1, para o cálculo da resistência de Thévenin a fonte de tensão fica curto-circuitada. Se fosse uma fonte de corrente, a mesma ficaria aberta.

$R_\mathrm{AB} = R_1 + \left [ \left ( R_2 + R_3 \right ) \| R_4 \right ) ]$

$= 1\,\mathrm{k}\Omega + \left [ \left ( 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \right ) \| 2\,\mathrm{k}\Omega \right ) ]$

$= 1\,\mathrm{k}\Omega + \left({1 \over ( 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega )} + {1 \over (2\,\mathrm{k}\Omega ) }\right)^{-1} = 2\,\mathrm{k}\Omega$

e a tensão de circuito aberto pode ser calculada usando a seguinte abordagem:

$V_\mathrm{AB} = {R_2 + R_3 \over (R_2 + R_3) + R_4} \cdot V_\mathrm{1}$

$= {1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega) + 2\,\mathrm{k}\Omega} \cdot 15 \mathrm{V}$

$= {1 \over 2} \cdot 15 \mathrm{V} = 7.5 \mathrm{V}$

Conversão do Equivalente de Thévenin no Equivalente de Norton

Os teoremas de Thévenin e de Norton são dois teoremas duais aplicáveis a circuitos lineares. O teorema de Norton estabelece que qualquer circuito linear visto de um ponto pode ser representado por uma fonte de corrente (igual à corrente do ponto em curto-circuito) em paralelo com uma impedância (igual à impedância do circuito vista desse ponto). A esta configuração chamamos configuração Norton, ou Equivalente de Norton.

Equivalente de Norton.

Decorre destes dois teoremas que uma configuração Thévenin pode ser transformada numa configuração Norton, e vice-versa, desde que Vo = Z Is.

Limitações dos teoremas de Thévenin e Norton

Teorema de Norton

O teorema de Norton para circuitos elétricos afirma que qualquer coleção de fontes de tensão, fontes de corrente, e resistores, com dois terminais é eletricamente equivalente a uma fonte de corrente ideal, I, em paralelo com um único resistor, R.

Origem: Wikipédia, a enciclopédia livre.

http://www.4shared.com/zip/w9z2KN2C/thvenin___norton.html